欧几里得算法

在数学中，辗转相除法，又称欧几里得算法（英语：Euclidean algorithm），是求最大公约数的算法。辗转相除法首次出现于欧几里得的《几何原本》（第VII卷，命题i和ii）中，而在中国则可以追溯至东汉出现的《九章算术》。

过程

欧几里得算法基于一个非常简单的原理：对于两个数a和b(a > b)， a和b的最大公约数与b和a - b的最大公约数相同。

重复的迭代这个过程， 使$gcd(a,b)⟺gcd(b,a-b)$. 如此一来， 参数不断减小， 最后某时刻两个参数的值必然相等， 此时a、b的值即为最大公约数.

减运算代码实现

def gcd(a, b):
    if b == a: # 或 if b == 0, 因为b == a时再迭代一次后必然是gcd(a, 0)
        return a
    if a < b:
        return gcd(b, a)
    return gcd(a - b, b)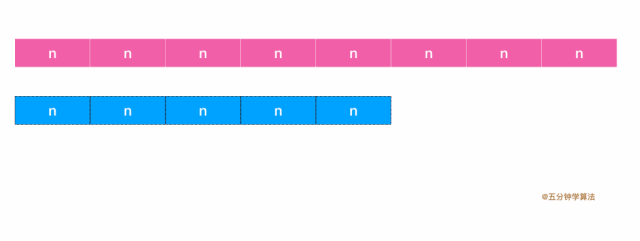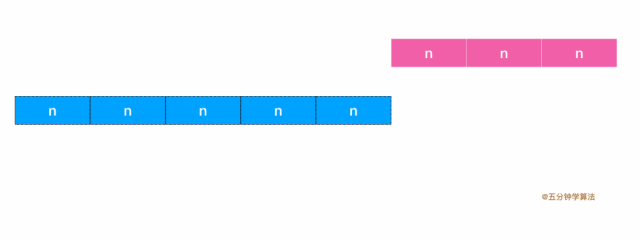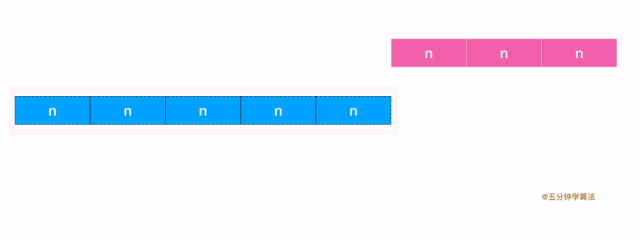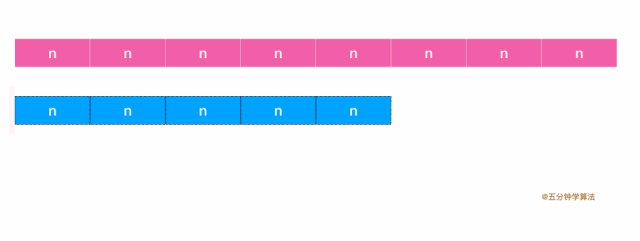

模运算

但一般情况下， 我们会使用模运算来减少迭代的次数。

设a(a > b)设为a = kb + c， c < b， 则用减法的欧几里得迭代过程的前面一部分显然是

$$gcd(kb+c,b)⟺gcd((k-1)b+c,b)⟺...⟺gcd(c,b)$$

上述过程可以简化为

$$gcd(a,b)⟺gcd(a\mathrm{\%}b,b)$$

由此我们可以写出用模运算代替减法运算的代码

模运算代码实现

python

def gcd(a, b):
    return a if b == 0 else gcd(b, a % b)

c++

int gcd(int a, int b) {
 return b ? gcd(b, a % b) : a;
}

一个比较巧妙的点是， 如果a < b， 则$gcd(a,b)⟺gcd(b,a\mathrm{\%}b)⟺gcd(b,a）$, 通过一次递归调整回了第一个参数较大的情况。

模运算的迭代过程相比减运算是跳跃式的， 所以不一定会经过a==b这个状态， 因此应该以b=0为结束条件。

欧几里得算法的时间复杂度为$O(logn)$, 因为对于a、b(a > b)， a %= b至少会让a减少一半以上。

扩展欧几里得算法

裴属定理

裴属定理：对于任意整数a、b， 都能找到两个整数x、y使得ax + by = gcd(a, b).

设a、b的最大公约数为c， 则有a = i * c, b = j * c, 且i、j互质。所以裴属定理的另一种形式是：对于两个互质的整数a、b， 都能找到两个整数x、y使得ax + by = 1。

过程

扩展欧几里得算法常用于寻找裴属定理的一组可行解。

设$a{x}_1+b{y}_1=gcd(a,b)$, $x_1$和$y_1$就是我们要求的解。

在欧几里得算法中， 如果要求$gcd(a,b)$， 会递归的求$gcd(b,a\mathrm{\%}b)$.

设$b{x}_2+(a\mathrm{\%}b)y_2=gcd(b,a\mathrm{\%}b)$.

$\because \ $$gcd(a, b) = gcd(b, a%b)$

$\therefore a{x}_1+b{y}_1=b{x}_2+(a\mathrm{\%}b)y_2$

又$\because a\mathrm{\%}b=a-b\ast \lfloor \frac{a}{b}\rfloor$

$\therefore a{x}_1+b{y}_1=b{x}_2+(a\mathrm{\%}b)y_2=b{x}_2+(a-b\ast \lfloor \frac{a}{b}\rfloor )y_2$

化简得$a{x}_1+b{y}_1=a{y}_2+b(x_2-y_2)\lfloor \frac{a}{b}\rfloor$, 所以$x_1=y_2,y_1=x_2-y_2\lfloor \frac{a}{b}\rfloor$.

要求$x_1,y_1$， 只需先递归的求出$x_2,y_2$即可。

在欧几里得算法的递归终点$gcd(c,0)$中, 要使$c{x}_3+0y_3=gcd(c,0)=c$, 一组可行的解是$x_3=1,y_3=0$。到达终点后， 不断回溯对$(x,y)$进行递推， 最后即可得到关于$(a,b)$的一组可行解。

代码实现

python

def exgcd(a, b):
    if b == 0: 
        return 1, 0
    x, y = exgcd(b, a % b)
    return y, x - y*(a // b)

c++

void exgcd(int a, int b, int &x, int &y) {
    if (b == 0) {
        x = 1, y = 0;
    } else {
        exgcd(b, a % b, x, y);
        int t = x;
        x = y, y = t - y * (a / b);
    }
}

参考

辗转相除法 - 维基百科，自由的百科全书 (wikipedia.org)

小知识：什么是「欧几里得算法」_吴师兄学算法 (cxyxiaowu.com)

最大公约数 - OI Wiki (oi-wiki.org)

裴蜀定理_百度百科 (baidu.com)

扩展欧几里得算法 - 维基百科，自由的百科全书 (wikipedia.org)