欧拉通路(路径): 一条经过了图中所有边的路径， 且每条边仅经过一次。 欧拉回路: 起点和终点相同的欧拉通路。 欧拉图: 存在欧拉回路的图 半欧拉图: 不存在欧拉回路， 但存在欧拉通路的图

之所以以欧拉的名字命名， 是因为欧拉解决了与此紧密相关的一笔画问题， 即在不重复、折返的情况下遍历一张无向图。

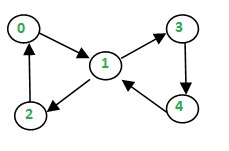
判别欧拉图

欧拉图的判断可以使用欧拉提出的“一笔画定理”。

连通的无向图有欧拉路径的充要条件是：$G$中奇顶点（连接的边数量为奇数的顶点）的数目等于0或者2。

连通的无向图是欧拉图（存在欧拉回路）的充要条件是：中每个顶点的度都是偶数。

证明可见:一笔画问题 - 维基百科

例题——欧拉路径

判断一无向图是欧拉图、半欧拉图还是非欧拉图 输入格式

第一行包含两个整数 N 和 M，表示无向图的点和边的数量。

接下来 M 行，每行包含两个整数 a,b，表示点 a 和 b 之间存在一条边。

所有点的编号从 1∼N。

输出格式 输出对该图的判断，Eulerian（欧拉图），Semi-Eulerian（半欧拉图），Non-Eulerian（非欧拉图）。

行尾不得有多余空格。

代码实现

• 使用并查集判断图是否连通
• 构造顶点的度数组， 用于判断欧拉图

#include <bits/stdc++.h>
using namespace std;
const int N = 510;
int p[N], d[N];
int n, m;

int find(int x) {
    if (x == p[x]) return x;
    return p[x] = find(p[x]);
}

//使用并查集判断图是否连通
bool isConnected() {
    for (int i = 2; i <= n; i ++) {
        if (find(i) != find(1)) return false;
    }
    return true;
}

//判断图中是否有欧拉路径
bool hasEulerianPath() {
    int odd = 0;
    for (int i = 1; i <= n && odd <= 2; i ++) {
        if (d[i] & 1) odd ++;
    }
    return odd == 0 || odd == 2;
}

//判断图中是否有欧拉回路
bool hasEulerianCircuit() {
    for (int i = 1; i <= n; i ++) {
        if (d[i] & 1) return false;
    }
    return true;
}

int main () {
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) p[i] = i;
    while (m --) {
        int a, b; cin >> a >> b;
        d[a] ++, d[b] ++;
        p[find(a)] = find(b);
    }
    
    if (!isConnected()) cout << "Non-Eulerian";
    else if (hasEulerianCircuit()) cout << "Eulerian";
    else if (hasEulerianPath()) cout << "Semi-Eulerian";
    else cout << "Non-Eulerian";
    
    return 0;
}

求欧拉回路

求欧拉回路一般使用Hierholzer算法。

Hierholzer算法的基本流程如下：

• 从任一点开始对图进行dfs遍历
• 遍历过程中经过的边直接删除
• 当一个顶点的出度减为0时， 加入栈中
• dfs结束后， 将栈中元素出栈， 即为一条欧拉回路

伪代码即为：

dfs(node u) {
    while (!u.edges.empty()) {
        node next = u.edges.back();
        u.edges.pop_back();
        dfs(next);
    }
    stk.push(u);
}

性质一： dfs的起点就是得到的欧拉回路的起点

性质二： 若要求从某起点出发、字典序最小的欧拉回路， 只需要在遍历边时贪心的选择顶点编号最小的边即可， 可以使用排序或优先队列。

例题——重新安排行程

给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。 假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

来源：力扣（LeetCode） 链接：https://leetcode.cn/problems/reconstruct-itinerary 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

Solution 显然这题是有向边求字典序最小的的欧拉回路。 由于顶点是用字符串代表， 所以用哈希表记录每个顶点的出边集。 预先对出边集排序， 在遍历时看最小的出边。

class Solution {
public:
    map<string, vector<string>> e;
    vector<string> stk;

    void dfs(string u) {
        while (e[u].size()) {
            string ne = e[u].back(); e[u].pop_back();
            dfs(ne);
        }
        stk.push_back(u);
    }

    vector<string> findItinerary(vector<vector<string>>& tickets) {
        for (auto &v : tickets) {
            e[v[0]].push_back(v[1]);
        }
        for (auto &[s, v] : e) {
            sort(v.begin(), v.end(), greater<>());
        }
        dfs("JFK");
        reverse(stk.begin(), stk.end());
        return stk;
    }
};