红黑树

由于c++里已经有现成的红黑树(map)，所以之前由于没有应用场景，一直没有去了解红黑树。

现在为什么会去学习红黑树:

js的map很不好用
1. 必须通过get、set函数操作值
2. 没有默认值
js的map底层是哈希表实现，导出的数据顺序是插入顺序(不符合直觉)
引用类型直接认为是不一样的，没有提供自定义hash值的接口

本来想找一些第三方库，但并没有找到比较好的, 于是打算自行填了红黑树这个坑, 实现工具自给自足。

前言: 红黑树是较为复杂的数据结构, 有比较多的背景知识, 所以本文将从科普平衡树的角度出发总结平衡树家族和红黑树由来。

BST(二叉搜索树)

二叉搜索树在二叉树的基础上增加了如下性质的要求:

空树是一颗二叉搜索树
二叉搜索树的左子树上任意结点的权值小于根结点
二叉搜索树的右子树上任意结点的权值大于根结点
二叉搜索树的左右子树均为二叉搜索树

从上面可以看出BST有个隐式的要求是不能出现两个权值相等的结点，对于这种情况的处理一般是根据场景选择<后来者覆盖前者>或者<添加结点count值>

BST可以很好的解决可变序列的搜索问题。试想一个数组里，它将来可能需要删除某个元素，也可能会添加进来一些元素，你需要在这些情况发生的同时满足较快的搜索。

BST的查找

将搜索值从根结点开始比较:

当前结点权值与搜索值相同: 找到了
当前结点权值小于搜索值：与左孩子进行比较
当前结点权值大于搜索值: 与右孩子进行比较
当前结点为空：查找失败，不存在

typescript

searchNode(root: N | null, key: K): N | null {
    if (root === null) return null;
    const compareResult = this.compare(root.key, key);
    switch (compareResult) {
      case COMPARE_RESULT.EQUAL:
        return root;
      case COMPARE_RESULT.LESS:
        return this.searchNode(root.left, key);
      case COMPARE_RESULT.MORE:
        return this.searchNode(root.right, key);
    }
  }

BST的添加操作与此类似，不再重复。

BST的删除

首先在搜索树中查找到待删除值对应的结点。

待删除结点为叶子结点: 直接删除即可
待删除结点只有一个儿子: 删除结点后，让唯一的儿子顶替其位置即可
待删除结点有两个儿子: 删除结点，使用其【前驱】或【后继】顶替其位置

重点解释【前驱】和【后继】是什么，以及为什么可以让它们顶替。

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
A((5)) --> B((3))
A --> C((7))
B --> D((2))
B --> E((4))
C --> F((6))
C --> G((8))

classDef commonNode fill: black,color: white,stroke:none
class A,B,C,D,E,F,G commonNode

以此树距离，此树的中序遍历序列为

2, 3, 4, 5, 6, 7, 8

对于( $5$ )来说， ( $4$ )和( $6$ )分别是它的前驱、后继，因为在中序序列中它们是( $5$ )的前后两个结点。

当( $5$ )被删除时，使用 ( $4$ )或( $6$ )来顶替它的位置，不会破坏搜索树的性质，以( $4$ )举例。

注: NIL表示占位的空节点

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph 删除5后
A((4)) --> B((3))
A --> C((7))
B --> D((2))
B --> NIL
C --> F((6))
C --> G((8))
end
subgraph 删除5前
a((5)) --> b((3))
a --> c((7))
b --> d((2))
b --> e((4))
c --> f((6))
c --> g((8))
end

classDef commonNode fill: black,color: white,stroke:none
class A,B,C,D,E,F,G,a,b,c,d,e,f,g,NIL commonNode

可以发现，由于( $4$ )满足

大于5左子树所有结点(除了4)
小于5右子树所有结点

所以4天然可以取代5的位置；6同理。

N的前驱和后继的定义可以简化为:N左子树中权值最大的结点、N右子树中权值最小的结点。

BST的最坏情况

BST进行搜索和删除的时间复杂度都与BST的高度h成正相关，因为搜索操作最坏情况下需要从根一直比较到最深的叶子，也就是h次比较。

即时间复杂度为 $O (h)$ ，而h在最好情况下为 $l o g N$ 级别，最坏情况下为 $N$ ，其中N为树的结点数量。

当BST为一条链时，搜索和插入的时间复杂度为 $O (N)$ ，这是不能接受的。

而且通过一个有序（或大致有序）的插入顺序，就能轻易使BST达到比较坏的情况。

1, 2, 3, 4, 5, 6, 7

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
A --> n1[NIL]
B --> n2[NIL]
C --> n3[NIL]
D --> n4[NIL]
E --> n5[NIL]
F --> n6[NIL]
A((1)) --> B((2))
B --> C((3))
C --> D((4))
D --> E((5))
E --> F((6))
F --> G((7))

classDef commonNode fill: black,color: white,stroke:none
class A,B,C,D,E,F,G,n1,n2,n3,n4,n5,n6 commonNode

平衡树

平衡树是改进的二叉搜索树, 不同的平衡树关于平衡的定义有所不同，但总的来说是在追求: 各个叶子的深度(从根到各叶子结点的简单路径长度)趋于相近/平衡 (让树的高度尽量低，不出现某分支的深度远远的超过其他分支的情况)。

自平衡树

自平衡树：在插入、删除过后会自动调整树结构使其满足平衡定义的平衡树。

自平衡树相比于二叉搜索树而言，多了插入和删除时的维护平衡操作。

平衡树 -> 插入或删除结点(通二叉搜索树) -> 平衡树失衡 -> 维护平衡

树的旋转

考虑如下BST:

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
A((2)) --> B((1))
A --> C((4))
C --> F((3))
C --> D((5))
D --> n2[NIL]
D --> E((6))

classDef commonNode fill: black,color: white,stroke:none
class A,B,C,D,E,F,G,n1,n2 commonNode

右分支深度明显的大于左分支深度, 此时我们需要调整，使这棵树更平衡、且不破坏BST性质。

此时便可以使用旋转, 旋转操作图示如下:

bst-rotate

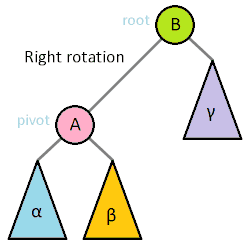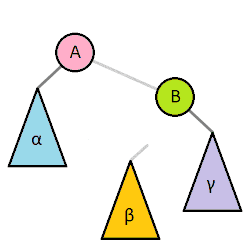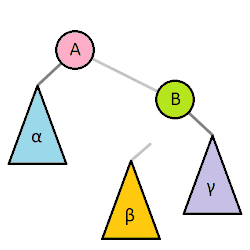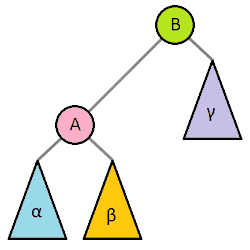
树旋转的过程演示

左旋、右旋的名字由来为根节点的移动方向，具体的:

左旋: 根结点移动到左子树上，根结点的右儿子成为了新的根结点。

右旋: 根结点移动到右子树上, 根结点的右儿子成为了新的根结点。

从结果上看:

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph after [左旋后]
a((4)) --> b((2))
b --> c((1))
a --> d((5))
b --> e((3))
d --> n1[NIL]
d --> f((6))
end
subgraph before [左旋前]
A((2)) --> B((1))
A --> C((4))
C --> F((3))
C --> D((5))
D --> n2[NIL]
D --> E((6))
end

classDef commonNode fill: black,color: white,stroke:none
class A,B,C,D,E,F,G,n1,n2,a,b,c,d,e,f commonNode

旋转操作不会破坏BST性质(中序不变)
左旋操作使原左子树深度+1，原右儿子右子树深度-1。 影响范围: (左+1、右右-1)
右旋操作使原右子树深度+1，原左儿子左子树深度-1。 影响范围: (右+1、左左-1)

旋转操作是大多数平衡树维护平衡性质的操作，时间复杂度为 $O (1)$ 。

typescript

/**
   * 左旋操作
   * @param node 左旋的子树根结点, 需要保证不为空且右子树不为空 
   * 
   *        g           p
   *       / \         / \
   *      u   p  -->  g   n
   *         / \     / \    
   *        m   n   u   m     
   */
rotateLeft(node: Node<K, V>) {
  const parent = node.parent;
  const direction = node.direction();
  const successor = node.right!;
  // 左旋核心操作, 根变为successor的左子树, successor变为根
  node.setRightChild(successor.left);
  successor.setLeftChild(node);

  // node的位置为successor取代, 需要更新node的父结点与successor的关系
  switch (direction) {
    case DIRECTION.LEFT:
      parent!.setLeftChild(successor);
      break;
    case DIRECTION.RIGHT:
      parent!.setRightChild(successor);
      break;
    case DIRECTION.ROOT:
      this.root = successor;
      break;
  }
}

AVL树

AVL树的平衡定义: 对于树中任意一个结点, 其左子树深度和右子树深度的差值绝对值不大于 $1$ .

平衡因子：右子树高度 - 左子树高度

AVL树名字的来源为它的两个发明者名字合并: Georgy Adelson-Velsky and Evgenii Landis

AVL树的性质保证了AVL树的高度为 $l o g N$ 级别, 因此也被称为『高度平衡树』。

AVL树的维护操作

先说明几个事实

插入/删除结点后，可能导致包含该结点的所有子树树失衡
由于是在AVL树上插入/删除了一个结点，所以若一颗子树失衡, 其 $| 平衡因子 |$ 只能为2

在AVL树插入/删除后, 我们将从插入/删除的结点的父结点开始向上(这样就能遍历到包含该结点的所有树)，判断当前当前节点的平衡因子是否失衡，若失衡则对当前结点进行维护。

维护操作可以分类讨论，一些约定如下:

所绘图中根结点（N）为失衡的结点(即h(L) - h(R) == 2 / -2)
L为N的左孩子、LL为L的左孩子(R、RR同理)
结点名称后用括号注明高度
『圆』为具体结点，而梯形代指一颗树

一些事实如下:

由于是自底向上进行维护，当前讨论的是结点N, 那么L所在子树和R所在子树已经维护完成符合AVL树性质
被插入/删除结点的爷爷结点开始，才可能出现失衡

LL/RR型失衡

以LL型失衡举例, 这是一颗LL型失衡的树, 满足如下特征:

N的左子树比右子树高
L的左子树比右子树高 --> $H (L L) \geq H (L R)$

设 $H (R) = h$ ，则有

$H (L) = h + 2$
$H (L L) = h + 1$
$h \leq H (L R) \leq h + 1$

此时L和R的高度差可以看成是LL和R的高度差，而右旋的效果为 (右+1、左左-1)满足此情况，进行一次右旋即可。

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph gb [右旋后]
A --> D[/"LL (h + 1)"\]
A((L)) --> B(("N (h+1 / h+2)"))
B --> E[/"LR (h / h+1)"\]
B --> C[/"R (h)"\]
end
subgraph ga [失衡]
a(("N")) --> b(("L (h+2)"))
a --> c[/"R (h)"\]
b --> d[/"LL (h+1)"\]
b --> e[/"LR (h / h+1)"\]
end

classDef commonNode fill: black,color: white,stroke:none
class A,B,C,D,E,F,G,H,I,J,K,L,M,N,n1,n2,n3,n4,n5,n6,n7,n8,a,b,c,d,e,f,g,h,i,j,k,l,m,n commonNode

右旋后LL、LR、R的高度并不会变化，此时我们可以计算出N的高度变为了 $h + 1 \leq H (N) \leq h + 2$ , N子树和L子树都满足了AVL树性质，修复完成!

LR/RL型失衡

同样只以LR型举例:

设 $H (R) = h$ , 则有

$H (L) = h + 2$ ;
$H (L L) = h$
$H (L R) = h + 1$
$h - 1 \leq H (L R L) \leq h$
$h - 1 \leq H (L R R) \leq h$

$L R / R L$ 型的失衡可以通过 L左旋 -> N右旋来解决，如下图

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
  subgraph gc [L左旋 + N 右旋后]
  k(("LR"))
  i(("L (h+1)"))
  h(("N (h+1)"))
  j[/"LL (h)"\]
  l[/"R (h)"\]
  m[/"LRL (h / h-1)"\]
  n[/"LRR (h / h-1)"\]
 
 k --> i
  k --> h
  i --> j
  i --> m
  h --> n
  h --> l
  end

  subgraph gb [L左旋后]
  A(("N"))
  B(("L (h + 1)"))
  D[/"LL (h)"\]
  E(("LR (h+2)"))
  C[/"R (h)"\]
  F[/"LRL (h / h-1)"\]
  G[/"LRR (h / h-1)"\]
  A --> E
  A --> C
  E --> B
  B --> D
  B --> F
  E --> G
  end

  subgraph ga [失衡]
  a(("N")) --> b(("L (h+2)"))
  a --> c[/"R (h)"\]
  b --> d[/"LL (h)"\]
  b --> e(("LR (h+1)"))
  e --> f[/"LRL (h / h-1)"\]
  e --> g[/"LRR (h / h-1)"\]
  end


classDef commonNode fill: black,color: white,stroke:none
class A,B,C,D,E,F,G,H,I,J,K,L,M,N,n1,n2,n3,n4,n5,n6,n7,n8,a,b,c,d,e,f,g,h,i,j,k,l,m,n commonNode

从结果上看, 操作完成后 $H (L) = h + 1, H (N) = h + 1$ ，符合AVL树性质。

Todo: 是怎么想到用先后两次不同的旋转来修复性质的?是否蕴含着数学原理

B树

B树是一种自平衡多叉树。

一颗 $m$ 阶B树满足如下性质:

每个结点最多有 $m$ 个子结点
每个非叶子结点(除了根)至少有 $⌈ m / 2 ⌉$
如果根节点不是叶子节点，那么它至少有两个子节点。
若一个结点有有k个子结点，那么该结点有k-1个键，反之亦然；
每个结点的键值升序排列，且n的第k个子节点的所有键值满足小于n的第k个键值、大于n的第k-1个键值
所有的叶子节点都在同一层。

红黑树是满足如下性质的二叉搜索树:

每一个结点要么是红色，要么是黑色
红色结点的孩子必须为黑色
对于红黑树中任意一个结点，它到NIL(null)结点的每一条简单路径必须包含相同数量的黑色结点

除此之外，还有两条被广泛使用的红黑树的性质

根结点是黑色
NIL(null)结点被认为是黑色

这两条性质对于红黑树来说并不是必须的，但能便利对红黑树的算法归纳，我们姑且也认为这是红黑树必须满足的性质。

红黑树最初是从B树中推导出来的, 事实上红黑树可以等价的看做四阶B树。

红黑树与4阶B树

以下引用自: 红黑树 | Jason‘s Blog (jasonxqh.github.io)

红黑树和4阶B树之间存在等价关系。如哦从红黑树的树根开始，自顶向下逐层检查，如果遇到红结点，则将该节点压缩到父节点一侧；如果遇到黑节点，则保留。因为红结点对黑高没有贡献，而黑结点对黑高有贡献。
红黑树与4阶B树的4种等价方式：
1）两个黑孩子(黑黑)，如图所示：
2）左黑右红(黑红)，如图所示：
\3) 左红右黑(红黑) ，如图所示：
4）两个红孩子(红红)，如图所示
从红黑树与4阶B树的等价关系可以看出，4阶B树中的结点中必然含有一个黑节点。而且不会出现红色的父亲。每一个结点最多包含三个关键字：如果包含2个红关键字，则黑关键字必然在中间位置。
我们可以尝试将这一棵红黑树进行压缩。
最后可以得到这样一棵4阶的B树
那么既然红黑树和4阶B树是可以互相转化的，那么为什么还要用红黑树呢？这是因为红黑树和B树处理的方向不同。B树主要用于内外存的访问，旋转不是很容易，但是红黑树的旋转调平衡比较方便

插入

红黑树的插入，首先将插入结点按照BST的规则插入树中，然后判断是否会导致失衡，根据其情况使用不同策略进行修正。

一些约定:

N为插入的结点
P为parent父亲结点
G为grandparent爷爷结点
U为uncle叔叔结点
圆形结点为具体的节点；梯形结点代表一颗无需透露细节的子树
结点名称后如有括号，则表示该节点到叶子结点的黑色数量

一些事实:

插入的结点必然为红色结点。因为被插入的树已经满足红黑树性质，此时如果插入一个黑色结点，那么必然会让某条路径的黑色数量+1，造成失衡(除空树情况)
空树情况下，将插入结点更改为黑色即可
插入结点的父亲为黑色时，不会破坏红黑树性质。

排除以上情况时，必然满足:

插入结点有父结点且父结点为红色
插入结点有爷爷且爷爷为黑色

接下来我们将以uncle为红/黑时分类讨论剩下的失衡情况。

uncle为红色时

此时我们将G染红， P和U染黑，此时G子树已经修正了性质，但G变红可能导致更上层的失衡，因此我们将G当成刚插入的结点，递归地维护。

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph 换色后
g((G))
p((P))
u((U))
n((N))
pr[/ \]
nl[/ \]
nr[/ \]
ul[/ \]
ur[/ \]

g --> p
g --> u
p --> n
p --> pr
n --> nl
n --> nr
u --> ul
u --> ur
end
subgraph 失衡状态
G((G))
P((P))
U((U))
N((N))
PR[/ \]
NL[/ \]
NR[/ \]
UL[/ \]
UR[/ \]

G --> P
G --> U
P --> N
P --> PR
N --> NL
N --> NR
U --> UL
U --> UR
end

classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class G,p,u blackNode
class P,N,U,g,n redNode
class PR,NL,NR,UL,UR,pr,nl,nr,ul,ur tree

typescript

if (uncle && uncle.isRed()) {
  uncle.setBlack();
  parent.setBlack();
  gparent.setRed();
  this.maintainAfterInsert(gparent);
  return;
}

uncle为黑色时: LL/RR型失衡

以LL型失衡举例(P为G的左儿子， N为P的左儿子)

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
G((G))
P((P))
U((U))
N((N))
PR[/ \]
NL[/ \]
NR[/ \]
UL[/ \]
UR[/ \]

G --> P
G --> U
P --> N
P --> PR
N --> NL
N --> NR
U --> UL
U --> UR
classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class G,U blackNode
class P,N redNode
class PR,NL,NR,UL,UR tree

我们从4阶B树的角度上看(B树的图非常重要非常好):

在不破坏搜索树性质的情况下，如上B树只需交换p、g颜色即可。

回收前文的一些疑问:
为什么要分uncle为红还是黑？
由上图可以发现，当uncle为红时， x-p-g这一层还要加一个u变成 x-p-g-u
4阶B树的结点键值数超过了3，此时发生上溢，需要进行分裂操作，如上图。
g变为红色后, g的上层可能失衡，因此需要递归向上解决。
叶子结点为什么要认为是黑色?
在解决红黑树的失衡过程中，经常遇到需要根据某个结点的颜色分类讨论的情况, 但我们发现，讨论结点的颜色其实只是在区分红色(B树形式中会压缩到父结点) / 非红色(不会在父结点中) 两种情况。
所以没有必要每次都加一条: 如果为空，如何如何。

而由于4阶B树形式中黑色为根结点，换成二叉树操作需要分为两步:

基于g进行右旋
将p染黑， g染红

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph 右旋 + 换色后
p((P))
u((U))
n((N))
g((G))
pr[/ \]
nl[/ \]
nr[/ \]
ul[/ \]
ur[/ \]

p --> n
n --> nl
n --> nr
p --> g
g --> pr
g --> u
u --> ul
u --> ur
end
subgraph 失衡状态
G((G))
P((P))
U((U))
N((N))
PR[/ \]
NL[/ \]
NR[/ \]
UL[/ \]
UR[/ \]

G --> P
G --> U
P --> N
P --> PR
N --> NL
N --> NR
U --> UL
U --> UR
end

classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class G,p,u blackNode
class P,N,U,g,n redNode
class PR,NL,NR,UL,UR,pr,nl,nr,ul,ur tree

typescript

if (parent.direction() === node.direction()) {

  if (node.direction() === DIRECTION.LEFT) {
    // LL型失衡
    this.rotateRight(gparent);
  } else {
    // RR型失衡
    this.rotateLeft(gparent);
  }

  parent.setBlack();
  gparent.setRed();
}

uncle为黑色时: LR/RL型失衡

以LR型失衡举例(P为G的左儿子， N为P的右儿子):

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
G((G))
P((P))
U((U))
PL[/ \]
N((N))
NL[/ \]
NR[/ \]
UL[/ \]
UR[/ \]

G --> P
G --> U
P --> PL
P --> N
N --> NL
N --> NR
U --> UL
U --> UR
classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class G,U blackNode
class P,N redNode
class PL,NL,NR,UL,UR tree

同样转化为4阶B树形式:

同样是出现了连续的红色，同样把中间染黑，但LR要进行的操作要多一点：

基于P进行左旋

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph P左旋后
g((G))
p((P))
n((N))
u((U))
pl[/ PL \]
nl[/ NL \]
nr[/ NR \]
ul[/ UL \]
ur[/ UR \]

g --> n
g --> u
n --> p
n --> nr
p --> pl
p --> nl
u --> ul
u --> ur
end
subgraph 失衡状态
G((G))
P((P))
U((U))
PL[/ PL \]
N((N))
NL[/ NL \]
NR[/ NR \]
UL[/ UL \]
UR[/ UR \]

G --> P
G --> U
P --> PL
P --> N
N --> NL
N --> NR
U --> UL
U --> UR
end
classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class G,U,g,u blackNode
class P,N,p,n redNode
class PL,NL,NR,UL,UR,pl,nl,nr,ul,ur tree

基于G右旋
将N染黑, 将G染红

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD

subgraph "P左旋 + G右旋 + N、G换色后"
P((P))
G((G))
N((N))
U((U))
PL[/ PL \]
NL[/ NL \]
NR[/ NR \]
UL[/ UL \]
UR[/ UR \]

N --> P
P --> PL
P --> NL
N --> G --> NR
G --> U
U --> UL
U --> UR
end
subgraph P左旋后
g((G))
p((P))
n((N))
u((U))
pl[/ PL \]
nl[/ NL \]
nr[/ NR \]
ul[/ UL \]
ur[/ UR \]

g --> n
g --> u
n --> p
n --> nr
p --> pl
p --> nl
u --> ul
u --> ur
end

classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class G,U,g,u,N blackNode
class P,p,n,G redNode
class PL,NL,NR,UL,UR,pl,nl,nr,ul,ur tree

删除

在删除过程中，我们现对欲删除的键值进行搜索，在搜索到的节点为N的情况下:

若N有两个孩子，将其前驱(或后继)结点的键与值与N替换(不替换颜色)，此时要删除的结点改为了前驱(或后继)结点

经过了(1)，我们确认了要删除的结点究竟是哪个, 接下来以N代指要删除的结点, 此时我们继续分情况讨论:

若N为树中唯一的结点，直接删除即可

若N有左/右孩子, 删除N后用它的左/右孩子代替N的位置(由于前驱或后继的性质, N不可能有两个孩子)

(2)、`(3)策略保证了删除后BST的性质正确, 接下来从红黑树性质上考虑删除后如何修正:

若N为红色, 不会破坏红黑树性质，无需维护

当删除一个红色结点时, 并不会改变路径中黑色结点的数量；同时顶替它位置的左/右孩子和父亲(如果存在) 必然是黑色结点, 不会破坏红色结点的孩子必须为黑色的性质

若N有孩子
N的孩子必然为红色，否则N子树不满足红黑树性质

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph 删除N后
p((P))
pl[/"PL(k)"\]
r(("R(k-1)"))
rl[NIL]
rr[NIL]
p --> pl
p --> r
r --> rl
r --> rr
end
subgraph 删除N前
P((P))
PL[/"PL(k)"\]
N(("N(k)"))
R(("R(k-1)"))
NR[NIL]
RL[NIL]
RR[NIL]

P --> PL
P --> N
N --> R
N --> NR
R --> RL
R --> RR
end

classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class G,U,N,NR,rl,rr,RL,RR blackNode
class R,r,p,P redNode
class PL,NL,UL,UR,pl tree

删除N后, N所在路径的黑色数量减少，必然导致不同路径的黑色数量不同；且当P为红色时，又破坏了红结点孩子必须为黑结点的性质。

此时我们将R染黑，就同时解决了两条性质的失衡问题:

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph R染黑后
p((P))
pl[/"PL(k)"\]
r(("R(k)"))
rl[NIL]
rr[NIL]
p --> pl
p --> r
r --> rl
r --> rr
end
subgraph R染黑前
P((P))
PL[/"PL(k)"\]
R(("R(k-1)"))
RL[NIL]
RR[NIL]

P --> PL
P --> R
R --> RL
R --> RR
end

classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class G,U,N,NR,r,rl,rr,RL,RR blackNode
class R,p,P redNode
class PL,NL,UL,UR,pl tree

删除操作修正原理

让我们思考删除一个黑色结点N造成的后果, 本质上就是P(N的父亲)的两颗子树的黑色深度不再相等(N所在子树黑色深度减一)，此时解决方法无非:

在保证P树黑色深度不变的情况下，弥补N所在子树减少的黑色深度, 此时必然需要有一个红色结点被染成了黑色结点
- 被染黑的红色结点哪里来?
  - 在N所在子树上，代替N位置
  - 在S子树上, 需要调整结构让N子树多一个黑色结点
  - P染黑, S染红
(1)无法实现的情况下, 维护两颗子树黑色深度相同且将P树整体的黑色深度减一，此时相当于"P被删了"，向上递归维护。

我想表达的意思是, 删除黑色叶子结点后的维护操作, 应该将其看作一个整体、一颗子树的黑色深度减一，但它内部依然符合红黑树性质，这样去理解，进而复用到更广的情况。

我们重回(5)的情况, 5的情况本质是N子树的黑色数量减了1，所以用了一个本身在N子树上的红色结点染黑进行替代

而在N子树内部解决不了问题，就将问题抛给了上层。

P为红色, S和S两个孩子均为黑色

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph 维护后
p((P))
n((N))
s((S))
sl((SL))
sr((SR))
p --> n
p --> s
s --> sl
s --> sr
end
subgraph 失衡
P((P))
N((N))
S((S))
SL((SL))
SR((SR))

P --> N
P --> S
S --> SL
S --> SR
end
classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class P,s redNode;
class S,N,SL,SR,p,sl,sr,n blackNode;
class PL,NL,UL,UR,pl tree

此时将P染黑、S染红, 显然符合:

P子树和S路径黑色深度不变
s子树红黑树性质未遭到破坏
N路径黑色深度+1

即成功的为N擦了屁股。

typescript

sibling.setRed();
parent.setBlack();

P为黑色， S和S两个孩子均为黑色

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph 维护后
P((P))
N((N))
S((S))
SL((SL))
SR((SR))

P --> N
P --> S
S --> SL
S --> SR
end
subgraph 失衡
p((P))
n((N))
s((S))
sl((SL))
sr((SR))
p --> n
p --> s
s --> sl
s --> sr
end
classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class S redNode;
class S,N,SL,SR,p,sl,sr,n,s,P blackNode;
class PL,NL,UL,UR,pl tree

我们将S染红， P的两条路径下的黑色深度都减一, 将问题抛给上层。

typescript

sibling.setRed();
this.maintain(parent.parent);

P任意, S为黑色， N远侄为红色, 近侄任意

当N为P左儿子时， S的左儿子为近侄，右儿子为远侄；反之同理。

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph 维护后
P((P))
N((N))
S((S))
SL((SL))
SR((SR))

S --> P
P --> N
S --> SR
P --> SL
end
subgraph 失衡
p((P))
n((N))
s((S))
sl((SL))
sr((SR))
p --> n
p --> s
s --> sl
s --> sr
end
classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class sr redNode;
class N,SR,n,s,P blackNode;
class PL,NL,UL,UR,pl,sl,p,SL,S tree

P向N方向旋转
S和P交换颜色, 远侄染黑

此时各方面都满足性质

P任意, N近侄为红色，远侄为黑色

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph 维护后
p((P))
n((N))
sll[/ \]
slr[/ \]
s((S))
sl((SL))
sr((SR))
p --> n
p --> sl
sl --> sll
sl --> s
s --> slr
s --> sr

end
subgraph 失衡
P((P))
N((N))
S((S))
SL((SL))
SR((SR))

P --> N
P --> S
S --> SL
S --> SR

end
classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class SL,s redNode;
class N,SR,n,S,sr,sl blackNode;
class PL,NL,UL,UR,pl,p,P,sll,slr tree

将S向远侄方向右旋
将近侄染黑， S染红

此时情况变为了P任意, S为黑色， N远侄为红色, 近侄任意, 用同样方法解决即可。

以上四种情况，我们枚举完了S为黑色的所有情况, 接下来考虑S为红色的情况

S为红色

此时P和S的孩子只能为黑色, 且S必然有真实孩子

P向N方向旋转
P染红, S染黑

mermaid

%%{ init: { 'flowchart': { 'curve': 'basis' } } }%%
flowchart TD
subgraph 维护后
s((S))
p((P))
sr((SR))
n((N))
sl((SL))

s --> p
p --> n
p --> sl
s --> sr
end
subgraph 失衡
P((P))
N((N))
S((S))
SL((SL))
SR((SR))

P --> N
P --> S
S --> SL
S --> SR
end
classDef tree fill: white, color: black, stroke: black
classDef blackNode fill: black,color: white,stroke:none
classDef redNode fill: red,color: white,stroke: none
class S,p redNode;
class N,P,SL,SR,s,n,sl,sr blackNode;
class PL,NL,UL,UR,pl tree

此时可以发现整棵树相比之前的变化就是N下移， sibling变为了SL，其他部分并未失衡。

继续在新的P子树上继续维护即可。

typescript

if (sibling.isRed()) {
  if (direction === DIRECTION.LEFT) {
    this.rotateLeft(parent);
  } else {
    this.rotateRight(parent);
  }
  sibling.setBlack();
  parent.setRed();
  this.afterErase(parent);
}

红黑树和AVL树的比较

如果插入一个node引起了树的不平衡，AVL和RB-Tree都是最多只需要2次旋转操作，即两者都是O(1)；但是在删除node引起树的不平衡时，最坏情况下，AVL需要维护从被删node到root这条路径上所有node的平衡性，因此需要旋转的量级O(logN)，而RB-Tree最多只需3次旋转，只需要O(1)的复杂度。
AVL的结构相较RB-Tree来说更为平衡，在插入和删除node更容易引起Tree的unbalance，因此在大量数据需要插入或者删除时，AVL需要rebalance的频率会更高。因此，RB-Tree在需要大量插入和删除node的场景下，效率更高。自然，由于AVL高度平衡，因此AVL的search效率更高。

参考

rbtree.c-linux源码

红黑树 - OI Wiki (oi-wiki.org)

红黑树（图解+秒懂+史上最全） - 疯狂创客圈 - 博客园 (cnblogs.com)

红黑树 | Jason‘s Blog (jasonxqh.github.io)

数据结构-B树与红黑树 - Shuzang's Blog

Red–black tree - Wikipedia

The-Art-Of-Programming-By-July-2nd/ebook/zh/03.01.md at master · julycoding/The-Art-Of-Programming-By-July-2nd (github.com)

平衡树 - 维基百科，自由的百科全书 (wikipedia.org)

Weiss M A. 数据结构与算法分析 C语言描述（第2版）. 冯舜玺译. 机械工业出版社, 2004.

红黑树参考代码

见: trudbot/easy-map (github.com)

BST(二叉搜索树) ​

BST的查找 ​

BST的删除 ​

BST的最坏情况 ​

平衡树 ​

自平衡树 ​

树的旋转 ​

AVL树 ​

AVL树的维护操作 ​

LL/RR型失衡 ​

LR/RL型失衡 ​

B树 ​

红黑树 ​

红黑树与4阶B树 ​

插入 ​

uncle为红色时 ​

uncle为黑色时: LL/RR型失衡 ​

uncle为黑色时: LR/RL型失衡 ​

删除 ​

删除操作修正原理 ​

红黑树和AVL树的比较 ​

参考 ​

红黑树参考代码 ​

BST(二叉搜索树)

BST的查找

BST的删除

BST的最坏情况

平衡树

自平衡树

树的旋转

AVL树

AVL树的维护操作

LL/RR型失衡

LR/RL型失衡

B树

红黑树

红黑树与4阶B树

插入

uncle为红色时

uncle为黑色时: LL/RR型失衡

uncle为黑色时: LR/RL型失衡

删除

删除操作修正原理

红黑树和AVL树的比较

参考

红黑树参考代码